中学3年の数学 1学期期末テスト 平方根の大小(基本~応用)
平方根で間違いやすいポイントをしっかり確認しよう!
平方根の学習をしていると、よく出てくるのが「±(プラスマイナス)」の使い方に関する疑問です。
「いつ±をつければいいのかわからない…」という声もよく聞きます。ここではその基本をわかりやすく整理していきましょう。
たとえば、次のような問題があります。
問題1【144の平方根を求めよ】
→ 答え【±12】
問題2【5の平方根を、根号を使って表せ】
→ 答え【±√5】
問題3【√36を根号を使わずに表せ】
→ 答え【6】
さて、この3つの問題の違いがわかるでしょうか?
ポイントは、「平方根を求めよ」と問われたときは±をつける ということです。平方根は「ある数を2乗して元の数になる数」を指しますが、実は2乗して同じ答えになる数は正の数と負の数の2つがあります。たとえば、12²=144 ですし、(−12)² も 144 になります。ですから、平方根を聞かれたときは ±12 という答えになるのです。
ただし、√(ルート)を含んだ形が与えられていて、それを計算するだけなら基本的に正の数(主値)だけを書くのが一般的です。たとえば √36 の計算結果は 6 です。
この基本ルールを押さえておけば、多くの平方根の問題は正しく解くことができます。
平方根を使った大小比較の問題に挑戦!
次に、平方根を使った少し応用的な問題を見てみましょう。
問題【√3と√5の間にある整数を答えよ】
→ 答え【2】
こういった問題では、まず 数直線をイメージすることが大事です。
そして、それぞれのルートの位置を下に書き入れていきます。
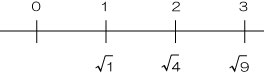
実際に √3 や √5 の位置を大まかに書き込んで整理します。
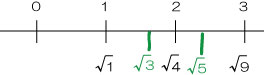
問題は「間にある整数は?」なので、上段の整数の並びを見れば、間にあるのは「2」とわかります。
さらにもう一問、応用問題!
問題【1<√a<3 を満たす整数 a をすべて求めよ】
こちらも、まずは数直線を引いて整理します。

次に、それぞれのルートの位置を下に記入します。

1と3の位置をしっかり把握します。
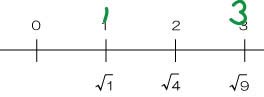
問題は「√aが1より大きく3より小さいときのaの整数値をすべて求めよ」です。
√aの世界では、次のように整理されます。
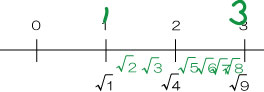
このことから、答えは【2,3,4,5,6,7,8】となります。
注意点として、「>」や「<」の記号は境界の数を含まないという意味なので、1や9は含まれません。一方、「≧」や「≦」であれば境界の数も含むことになります。
まとめ
平方根の学習は、最初は戸惑うこともありますが、
- 平方根を求めるときは±をつける
- ルート計算では基本的に正の値を出す
- 大小比較は数直線を使って考える
というポイントを押さえておけば、しっかり対応できます。
もし、まだ不安な点があれば、いつでもお気軽にご質問ください。無料でメール相談も承っていますので、一緒にスッキリ理解していきましょう!