中学3年 因数分解のテクニック
因数分解のテクニック(中3生向け)
「順番に出れば解けるのに、バラバラに出題されると手が止まる…」
そんな生徒はとても多いです。
実は、それは「どの公式を使えばいいか」がピンと来ていないだけ。
本質はそこまで難しくありません。
ここでは、因数分解に慣れていない中学生のために、ざっくりと使い分けを覚えるための“テクニック”をご紹介します。
ただし、あくまでも“近道”であって、“万能ではない”ことも忘れずに。
テクニック①:共通因数を見つけろ!
まずは「全部の項に共通しているもの」を探しましょう。
例:
6x² + 9x → 共通因数は3x → 3x(2x + 3)
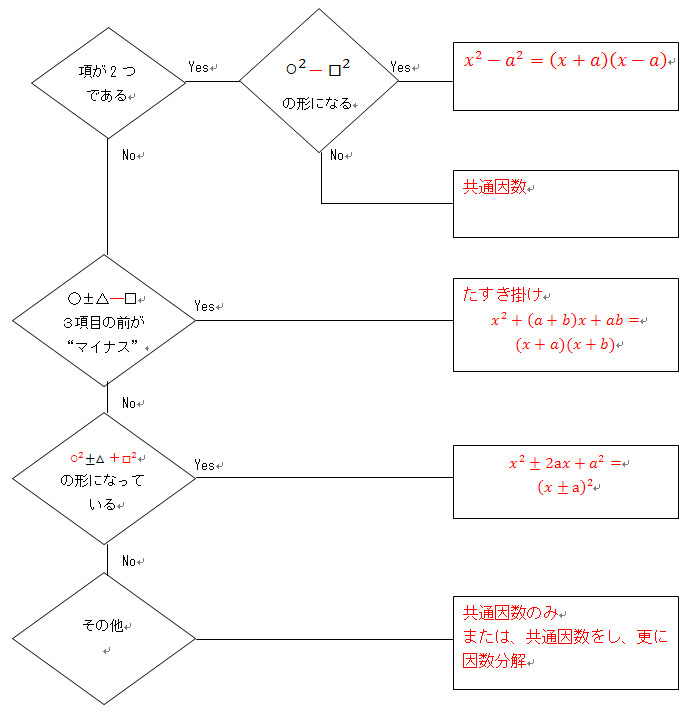
テクニック②:公式に当てはめてみる
以下の3つのパターンに“ざっくり”当てはまるかをチェックします。
- パターンA:a² – b²(差の2乗)
x² – 9 → x² – 3² → (x – 3)(x + 3) - パターンB:a² + 2ab + b²(平方の展開の逆)
x² + 6x + 9 → x² + 2×3x + 3² → (x + 3)² - パターンC:ax² + bx + c型(かけてc、たしてb)
x² + 5x + 6 → かけて6、たして5 → (x + 2)(x + 3)
練習問題(因数分解)
次の式を因数分解しなさい。
- 12x² + 20x
- x² – 16
- x² + 7x + 10
- x² + 8x + 16
- 3x² – 12
【解答・解説】
- 共通因数は 4x → 4x(3x + 5)
- 差の2乗 → x² – 4² → (x – 4)(x + 4)
- かけて10、たして7 → 2と5 → (x + 2)(x + 5)
- 平方の公式の逆 → x² + 2×4x + 4² → (x + 4)²
- 共通因数は3 → 3(x² – 4) → 3(x – 2)(x + 2)
まとめ:覚え方のコツ
因数分解は「どのパターンかに気づけるか」が最大のカギです。
最初は手が止まりやすいですが、“この式、どの型っぽい?”と“型の引き出し”を探す感覚を身につけていくと、どんどん早く解けるようになります。
このページのテクニックは「とっかかり」として使って、繰り返し問題に触れていきましょう!